文章地址:https://papers.nips.cc/paper/6948-collecting-telemetry-data-privately.pdf
标题:Collecting Telemetry Data Privately
作者:Bolin Ding, Janardhan Kulkarni, Sergey Yekhanin
发表会议:NIPS 2017
从用户那里搜集数据并进行统计分析是很重要的,也是和用户隐私密切相关的。传统情况下根据组合机制,对同一个数据持续收集会导致隐私保护程度的急剧下降。本文针对计数的数据,提出了基于LDP的数据收集方法,并且在收集的数据上可以对原始数据进行统计分析,支持均值估计(mean-estimation)和直方图估计(histogram estimation)。
本文的主要框架如下:
- 1 Introduction
- 1.1. Preliminaries and problem formulation
- 1.2. Repeated collection and over of privacy framework
- 2 Single-round LDP mechanisms for mean and histogram Estimation
- 2.1. 1-Bit Mechanism for mean estimation
- 2.2. d-Bit Mechanism for histogram estimation
- 3 Memoization for ontinual collection of counter
- 3.1. α-point rounding for mean estimation
- 3.2 Privacy definition using permanent memoization
- 4 Output Perturbation
- 5 Empirical Evaluation
- 6 反思与总结
Introduction
为了保护隐私,数据收集一般遵循着这么一个流程,首先对原始数据进行一个变换,再将变换之后的数据(暂且称为匿名数据吧)发送给数据接收者。因为收集的数据是需要进行使用的,所以我们需要在匿名的数据中反推出原始数据的信息。
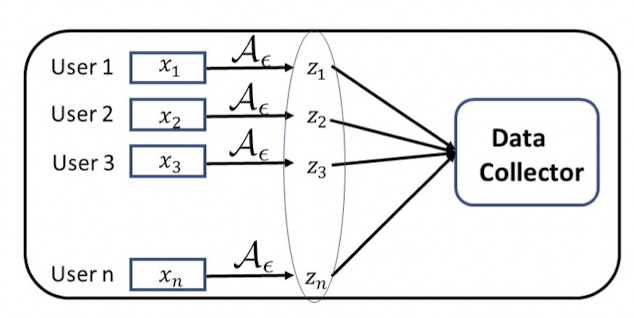
在数据收集的过程中,根据DP的组合机制,持续收集数据会使得隐私保护程度急剧降低。我们之前提过的RAPPOR就利用memoization来解决持续收集中的隐私保护下降问题。根据本文作者的阐述,RAPPOR存在这样的问题:
RAPPOR cannot allow for even very small but frequent changes in users’ private values, making it inappropriate for collecting counter data.
本文提出的方法就是针对counter data的数据收集方案,当用户的数据在小幅度变化的时候,依然可以有强有力的有效性保证。论文有以下贡献:
- 提出对于单次数据收集的1-bit机制,用来做均值估计和直方图估计。
- 提出了α-point round机制,可以用于长期数据收集(在这一点上,作者形容这个贡献用的technical contribution)。
- 本机制已经被微软用在了Win10当中对数据进行统计分析。
1.1 Preliminaries and problem formulation
既然要讨论数据收集的问题,就先要有一个假定,或者说问题背景:
假定有n个用户,每个用户在时刻t都有一个私密的counter数据,并且满足这个数据 $x_i(t)\in[0,m]$,所以数据收集者(我一般称之为服务器)收集到的数据就是这样的$\{x_i(t)\}_{i\in[n]}$,利用收集到的数据,服务器就可以进行对数据的统计分析。
当前的应用场景中我们是没有考虑到数据的隐私保护性的,接下来作者介绍了LDP的概念。
Definition 1. A randomized algorithm $\mathcal{A}:\mathcal{V}\rightarrow\mathcal{Z}$ is $\epsilon$-locally differentially private if for any pair of values $v, v’\in\mathcal{V}$ and any subset of output $S\subset \mathcal{Z}$, we have that:
和DP有关的概念这里就不在细述了,由于之前没有正式地介绍LDP和DP的差别,这里用直白的话说一下:DP的概念里面说的是去掉和不去掉任意一个元素对查询结果没有很大的影响,所以此元素的隐私得到保证。LDP里面说的是对于任意一个其他元素V’,对V的查询和对V’的查询结果相差不大,所以V和V’不好区分,由于对所有的V’都有这个性质,所以V是符合隐私保护要求的。实际上我理解的LDP的区别和DP的区别就是应用场景的限制。即我就是要收集数据,还没涉及到对数据集的查询,那么我们就用LDP来作为隐私保护的工具。
接下来作者就讲了本文要对数据的使用方法了,即数据是用来做均值估计和直方图估计的。简单理解来看均值估计就是要知道一串数据的均值,直方图估计就是要知道数据的直方图分布。
看起来也不费劲,我就将作者的话在这里贴一下,让读者明白数据是做什么的:
- Mean estimation: For each time stamp $t$, the data collector wants to obtain an estimation $\hat{\sigma}(t)$
for $\sigma(\vec{x_t}) = \frac{1}{n}\sum_{i\in[n] }x_i(t)$. The error of an estimation algorithm for mean is defined to be $\max_{\vec{x_t}\in[m]^n} |\hat{\sigma}(\vec{x_t})-\sigma(\vec{x_t})|$. In other words, we do worst case analysis. We abuse notation and denote $\sigma(t)$ to mean $\sigma (\vec{x_t})$ for a fixed input $\vec{x_t}$. - Histogram estimation: Suppose the domain of counter values is partitioned into k buckets (e.g., with equal widths), and a counter value $x_i(t)\in [0, m]$ can be mapped to a bucket number $v_i(t)\in[k]$. For each time stamp $t$, the data collector wants to estimate frequency of $v\in[k]:h_t(v) = \frac{1}{n} |{i:v_i(t)=v}|$ as $\hat{h}_t(v)$. The error of a histogram estimation is measured by $\max_{v\in[k]} |\hat{h}_t(v)-h_t(v)|$. Again, we do worst case analysis of our algorithms.
当然也顺带可以看一下作者是怎么做误差分析的,都是选取的worst case的相差结果作为误差。
1.2 Repeated collection and overview of privacy framework Privacy leakage in repeated data collection.
接下来就可以说一下本文数据收集框架图了:
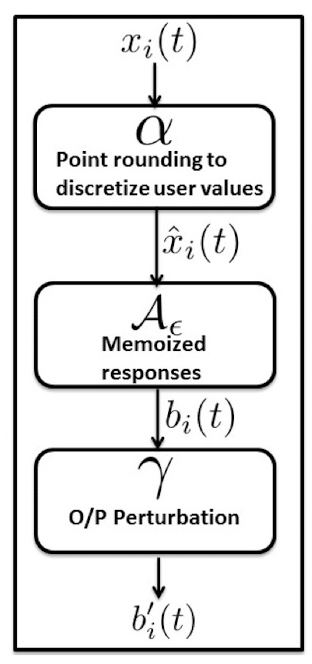
总的来说数据收集的过程中涉及4个组件:
- 1-bit机制组件,用于提供LDP的单次数据收集
- α-point round组件,用于将数据discretize,同时使得期望不变。
- 针对持续数据收集的Memoization组件
- 输出替代组件
2 Single-round LDP mechanisms for mean and histogram Estimation
这一节讲的是单次数据收集的方法,介绍了用于均值估计和直方图估计的1-Bit机制。
1-Bit Mechanism for mean estimation
在1-BitMean机制中,作者首先给出了满足epsilon-LDP的规则(天知道他咋想到这东西的,不过我们以后会介绍这东西咋想出来的)。然后介绍了这个机制的一些性质。
首先是1BitMean机制,由于涉及一些符号,我将原文摘抄下来:
Collection mechanism 1BitMean: When the collection of counter $x_i(t)$ at time $t$ is requested by the data collector, each user $i$ sends one bit $b_i(t)$, which is independently drawn from the distribution:
在阅读的1BitMean机制的时候,其实t可以省略,均值估计可以简化为这样一个过程:已知原始数据x_1, x_2, …, x_n,和其对应的满足LDP的变化b_1, b_2, …, b_n,如何在收到的b上面估计x的均值。
当然,给出了这个变化之后,作者给出了如何去估计均值:
Mean estimation: Data collector obtains the bits $\{b_i(t)\}_{i\in[n]}$ from $n$ users and estimates $\sigma(t)$ as:
细心的读者在给出了1BitMean之后,是可以很容易推导出公式(2)的,这里也就不说明了。
在均值估计中,接下来作者还分析了一下的几点:
- 1BitMean的误差分析(Theorem 1)
- 1BitMean是符合ε-LDP的(Lemma 1)
- 公式(2)的均值估计是无偏估计(Lemma 2)
- 1BitMean的误差分析(Lemma 3)
在证明的过程中,使用到了chernoff界,这是一个很重要的知识点,在很多和DP有关的证明中都有使用到。
d-Bit Mechanism for histogram estimation
好了,现在我们假定已经可以安全地估计出一系列数据的均值,然后基于这个性质,我们要做直方图估计,该怎么做呢?
首先,数据收集的过程是这样的:
Collection mechanism dBitFlip: Each user $i$ randomly draws $d$ bucket numbers without replacement from $[k]$, denoted by $j_1, j_2, …, j_d$. When the collection of discretized bucket number $v_i(t)\in[k]$ at time $t$ is requested by the data collector, each user $i$ sents a vector: $b_i(t)=[(j_1, b_{i, j_1}(t)), (j_2, b_{i, j_2}(t)), …, (j_d, b_{i, j_d}(t))]$, where $b_{i,j_p}$ is a random 0-1 bit with:
然后,根据收集到的数据,我们可以这样去估计直方图:
Histogram estimation: Data collector estimates histogram $h_t$ as: for $v\in[k]$:
因为这个机制论文里面说的不是很清楚,所以打算分一篇单独的推送来说一下。这里先挖个坑,让读者自己先思考一下,我以后再把这个坑补起来。
Memoization for continual collection of counter data
我们知道:当一个数据很小,或者这个数据变化范围很小的时候,重复查询得到的LDP保证的数据依然会有很大的精度或得到原始的数据。那么我们怎么解决这个问题呢?
其实在读到这里之前,我一直以为标题里面的memoization是memorization,还天真地以为是作者写错了,因为RAPPOR里面利用存储的方式来解决长期数据收集的问题,所以自然而然想到了记忆。读到这里才发现自己太naive了。
先来看下什么是memoization:
Memoization is a simple rule that says that: At the account setup phase each user pre-computes and stores his responses to data collector for all possible values of the private counter. At data collection users do not use fresh randomness, but respond with pre-computed responses corresponding to their current counter values. Memoization (to a certain degree) takes care of situations when the private value xi stays constant. Note that the use of memoization violates differential privacy. If memoization is employed, data collector can easily distinguish a user whose value keeps changing, from a user whose value is constant; no matter how small the ε is. However, privacy leakage is limited. When data collector observes that user’s response had changed, this only indicates that user’s value had changed, but not what it was and not what it is.
简单的来说是什么呢,就是对于计数数据,每个人现在本地按照一定规则计算出每个 x_i 对应的 x_i’,(这里要注意到的是,比如 1,用户 A 那里的 1 对应的 x’ 和用于 B 那里的 1 对应的 x’ 可能是不一样的),然后在数据上传的过程中,用户A的数据如果是1,那么就发送他对应的 x’。这种情况下,所有的 respond 都是 pre-computed,由于不是每次重新加入噪声,所以没有用到 fresh randomness。
所以如果一个人的数据保持不变,利用memoization可以很好地保证他的隐私保护需求。
文中提到,memoization和dp是冲突的,因为服务器可以很简单地区分这样两个用户:用户 A 的值保持不变,用户 B 的值存在变化。当然,也仅限于此,服务器仍然不知道具体的数值,所以 privacy leakage 依然是 limited。
在现实应用中,通常来说用户的 counter data 不是一成不变的,而是会在小范围内波动。因此这时候简单地加上DP就不太适用了。所以该怎么办呢:
一个想法就是分组嘛,比如数据分布为0-100,那么我分个十组,这样微小的变化依然是在一个分组里面,比如数据从在15-17之间变动,那么一直都在第二个分组里面。不过想都不用想,这个方法的局限很高。所以这里提供了一个更好的方法:α-point rounding。
α-point rounding for mean estimation
rounding的最关键作用就是将原始数据范围离散化(分组也是这么做的),但是离散化又不一定好(就像前面提到的分组)。离散化是会对数据准确性造成影响的,所以怎么办呢:making the discretization rule independent across different users。
所以基于1bitMean,作者又加上了α-point rounding,我们来看看怎么做的:
- 定义一个离散化系数s,同时我们假定s整除m(要是你非要问不整除咋办,那就重新回顾一下应用场景,m只是一个人为规定的数据范围)。s表示的含义是步长,m/s是分组个数。
- 每个用户从0到s-1这么多数之间单独选取一个值作为他本地的α值。
- 每个用户创建一个等差数列,形成很多区间,我待会会举给例子。
- 每个用户根据自己的等差数列将自己的值进行rounding操作,把数据归约到区间左边或者归约到区间右边。
好了,讲着这么多很绕口,举个例子就明白了。
我们假如数据分布范围为100,即m=100,然后s取10吧,挺标准的。那么m/s=10。这意味着把数据分成了10组。
这时候有个用户,他要选一个α,假如是α=2。
用户在本地创建一个等差数列(所有用户都是一样的):
A={0,10,20,30,40,50,60,70,80,90,100}
接下来就到数据的处理过程了,我们假如用户本地的数据是x=37,那么这时候先对37分组到原始数据中,因为37∈[30,40],所以L=30, R=40。接下来再看由于37+α<R,所以把x归约到30,否则就把x归约到40。
好,接下来我们再来看为什么这个方法依然可以做均值估计呢?实际上过程是这样的,我们先看这个图:
todo
然后思考这样一个问题,假如以a的概率将x归约到L,以b的概率将x归约到R,那么期望会怎么变化呢?可以由以下方程给出:
todo
所以上面的这个过程对于期望的估计依然是无偏的。实际上,α-point rounding 就是我所说的这个过程,其概率a即用的是x+α<R,因为α是随机选取的,和x无关,所以上述过程和α-point rounding是等价的。
定理三也就是把rounding和1BitMean结合起来,说这个过程依然是满足LDP的:
todo
其中论文中有一个拼写错误,已经改正了。
Privacy definition using permanent memoization
这一节大部分都是文字性和叙述性的东西,说实话,我也没有完全get懂。到3.4节这部分就先略过了,读者觉得有意思可以再和我讨论。
Output Perturbation
在输出前,还进行了一个output perturbation操作,实际上就是进一步替代。按照以下公式:
实际上,加上了Perturbation之后,就等价于以下式子:
读者也可以自行证明结合1BitMean和output perturbation之后,总的保护程度为:
实际上,这个是可以有一个通式可以表述出来的,我将会在Random Response中说明。在这里读者只需要知道这里是为了在喊噪声的结果之上进一步加噪就好了(一定要注意这个噪声是和原始数据有关的,比如你不能加一个Laplace噪声,因为Laplace噪声和数据是多少无关,会破坏原始数据的统隐私保护特性)。
Empirical Experiment
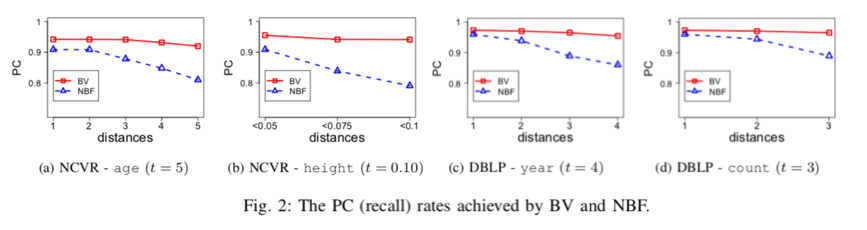
上图是 Mean Estimation 和Histogram Estimation的误差结果,其实怎么说呢,由于其统计特性,在数据量不那么大的时候其实误差还是比较大的。
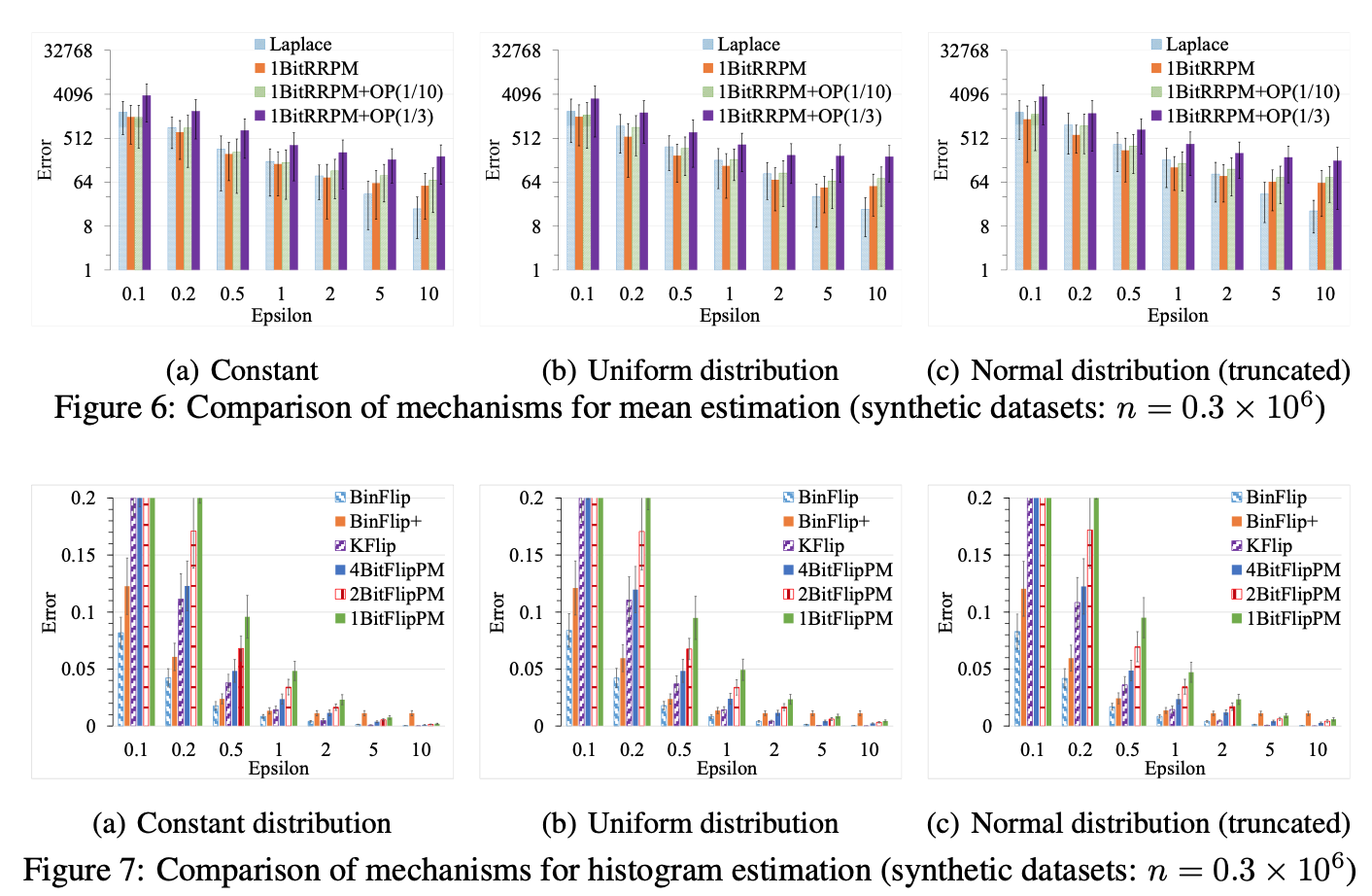
作者也看了不同数据分布下的误差,可以看到不同数据分布的实验效果其实是差不多的,毕竟方法在那里。
读论文的时候经常想到的一个问题是,作者是怎么想到的符合DP的机制的,比如本文中的1-bit机制。而不是给了你这个机制之后,你知道他是符合DP的。有的时候看到作者提出的机制,会感觉很奇妙:哇,这怎么想到的。
有的时候其实也是可以想到的。本来打算在本篇推送里面解释一下本文中作者的想法和公式的推导的,后来由于刘奇同学想单独写一篇random response的推送,所以就打算好好写一下random response了。
所以证明部分就先耽搁一下(反正一般证明过程也没人看~)。
当然,今天讲的这篇文章讲的比较粗泛,毕竟是NIPS上面的,我无法用很少的语言就把这个东西说明白,所以这次挖了几个坑需要我下次来补上:
- 1BitMean机制是怎么想到的?
- dBitFlip是如何做直方图估计的?
- Output Perturbation的privacy-preserving level通式推导。
每个坑我都会单独再给大家一一介绍。
本篇内容到这里就结束了,欢迎关注公众号《差分隐私》,获取更多前沿技术。


